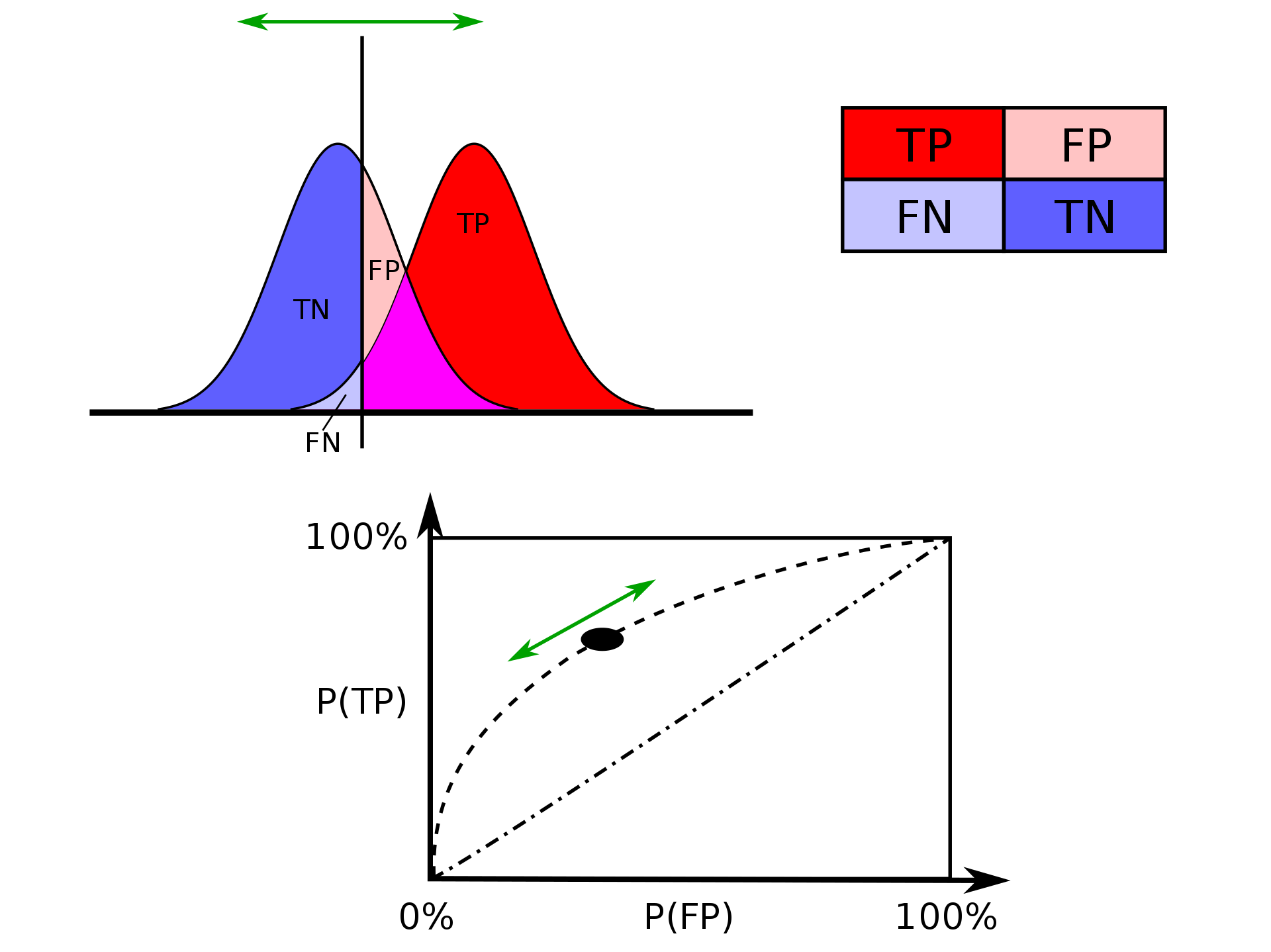
finding-thresholds-header

Classification with imbalanced class distributions is a major problem in machine learning. Researchers have given considerable attention to the applications in many real-world scenarios. Although several works have utilized the area under the receiver operating characteristic (ROC) curve to select potentially optimal classifiers in imbalanced classifications, limited studies have been devoted to finding the classification threshold for testing or unknown datasets. In general, the classification threshold is simply set to 0.5, which is usually unsuitable for an imbalanced classification. Here I showed, thresholds based on FPR-TPR, Precision-Recall-F1score, and Youden J-index in Python

Loading Libraries

# Loading libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from scipy import interp
from sklearn.preprocessing import scale
from sklearn.metrics import roc_auc_score, classification_report, accuracy_score, roc_curve, confusion_matrix, average_precision_score, precision_recall_curve
from sklearn.model_selection import cross_val_score, KFold, StratifiedKFold, train_test_split
from xgboost import XGBClassifier
import itertools
import glmnet
import xgboost as xgb

import seaborn as sns
sns.set_style("ticks")
mpl.rcParams['axes.linewidth'] = 3 
mpl.rcParams['lines.linewidth'] = 2
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:95% !important; }</style>"))
import warnings 
warnings.filterwarnings("ignore")
%matplotlib inline

Functions

#*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
# Function: _model

def _clf_train(X_train, y_train, X_test, y_test,
                 learning_rate = 0.05,
                 n_estimators = 100,
                 max_depth = 3,
                 min_child_weight = 5.0,
                 gamma = 1,
                 reg_alpha = 0.0,
                 reg_lambda = 1.0,
                 subsample = 0.9,
                 colsample_bytree = 0.9,
                 objective = "binary:logistic",
                 nthread = 4,
                 scale_pos_weight = 1.0,
                 seed = 1367,
                 random_state = 1367):
    """
    an xgboost model for training
    """

    clf = XGBClassifier(learning_rate = learning_rate,
                        n_estimators = n_estimators,
                        max_depth = max_depth,
                        min_child_weight = min_child_weight,
                        gamma = gamma,
                        reg_alpha = reg_alpha,
                        reg_lambda = reg_lambda,
                        subsample = subsample,
                        colsample_bytree = colsample_bytree,
                        objective = objective,
                        nthread = nthread,
                        scale_pos_weight = scale_pos_weight,
                        seed = seed,
                        random_state = random_state)
    
    clf.fit(X_train, y_train, eval_metric = "auc", early_stopping_rounds = 20, verbose = True, eval_set = [(X_test, y_test)])

    return clf

#*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
# Function: Finding thresholds
def _threshold_finder(model, X, y_true):
    """
    a function to find the optimal threshold for binary classification
    model: a trained model object (such as xgboost, glmnet, ...)
    X: the test set of features (pandas dataframe or numpy array)
    y_true: the true class labels (list or array of 0's and 1's)    
    """
    
    y_predict_proba = model.predict_proba(X)[:, 1]
    fpr, tpr, thresholds = roc_curve(y_true, y_predict_proba)
    auc = roc_auc_score(y_true, y_predict_proba)
    precision, recall, thresholds2 = precision_recall_curve(y_true, y_predict_proba)
    
    class_names = [0, 1]
    youden_idx = np.argmax(np.abs(tpr - fpr))
    youden_threshold = thresholds[youden_idx]
    y_pred_youden = (y_predict_proba > youden_threshold).astype(int)
    cnf_matrix = confusion_matrix(y_true, y_pred_youden)
    np.set_printoptions(precision=2)
    
    f1 = []
    for i in range(len(precision)):
        f1.append(2 * (precision[i] * recall[i]) / (precision[i] + recall[i]))
        
    queue_rate = []
    for thr in thresholds2:
        queue_rate.append((y_predict_proba >= thr).mean()) 

    plt.figure(figsize = (10, 5))
    plt.subplot(1,2,1)
    plt.plot(fpr, tpr, color = "red", label = F"AUC = {auc:.3f}")
    plt.plot(fpr[youden_idx], tpr[youden_idx], marker = "o", color = "navy", ms =10, label =F"Youden Threshold = {youden_threshold:.2f}" )
    plt.axvline(x = fpr[youden_idx], ymin = fpr[youden_idx], ymax = tpr[youden_idx], color = "navy", ls = "--")
    plt.plot([0,1], [0,1] , color = "black", ls = "--")
    plt.xlim([-0.01, 1.01])
    plt.ylim([-0.01, 1.01])
    plt.xlabel('1 - Specificity' , fontsize=12)
    plt.ylabel('Sensitivity' , fontsize=12)
    plt.tick_params(axis='both', which='major', labelsize=12)
    plt.legend( prop={'size':12} , loc = 4)

    plt.subplot(1,2,2)
    _plot_confusion_matrix(cnf_matrix, classes=class_names, normalize = False, cmap=plt.cm.Reds, title = F"Youden Threshold = {youden_threshold:.2f}\nAccuracy = {accuracy_score(y_true, y_pred_youden)*100:.2f}%")
    plt.show()
    
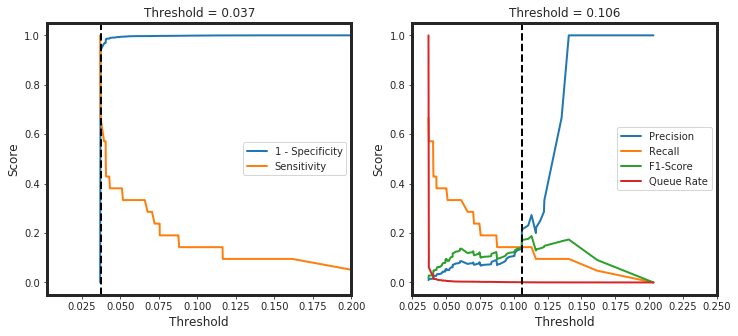
    plt.figure(figsize = (12, 5))
    plt.subplot(1,2,1)
    plt.plot(thresholds, 1-fpr, label = "1 - Specificity")
    plt.plot(thresholds, tpr, label = "Sensitivity")
    plt.xlabel("Threshold", fontsize = 12)
    plt.ylabel("Score", fontsize = 12)
    plt.legend(loc = 0)
    plt.xlim([0.025, thresholds[np.argmin(abs(tpr + fpr - 1))]+0.2])
    plt.axvline(thresholds[np.argmin(abs(tpr + fpr - 1))], color="k", ls = "--")
    plt.title(F"Threshold = {thresholds[np.argmin(abs(tpr + fpr - 1))]:.3f}", fontsize = 12)
    
    plt.subplot(1,2,2)
    plt.plot(thresholds2, precision[1:], label = "Precision")
    plt.plot(thresholds2, recall[1:], label = "Recall")
    plt.plot(thresholds2, f1[1:], label = "F1-Score")
    plt.plot(thresholds2, queue_rate, label = "Queue Rate")
    plt.legend(loc = 0)
    plt.xlim([0.025, thresholds2[np.argmin(abs(precision-recall))] + 0.2])
    plt.xlabel("Threshold", fontsize = 12)
    plt.ylabel("Score", fontsize = 12)
    plt.axvline(thresholds2[np.argmin(abs(precision-recall))], color="k", ls = "--")
    plt.title(label = F"Threshold = {thresholds2[np.argmin(abs(precision-recall))]:.3f}", fontsize = 12)
    plt.show()

#*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-
# Function: Plotting Confusion Matrix
def _plot_confusion_matrix(cm, classes,
                          normalize=False,
                          title='Confusion matrix',
                          cmap=plt.cm.Greens):
    from sklearn.metrics import precision_score, recall_score, roc_auc_score, accuracy_score, roc_curve, auc, confusion_matrix
    import itertools
    """
    This function prints and plots the confusion matrix.
    Normalization can be applied by setting `normalize=True`.
    """
    if normalize:
        cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]

    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title, fontsize = 14)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes)
    plt.yticks(tick_marks, classes)

    fmt = '.2f' if normalize else 'd'
    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, format(cm[i, j], fmt),
                 horizontalalignment="center",
                 color="black")

    plt.ylabel('True Class', fontsize = 14)
    plt.xlabel('Predicted Class', fontsize = 14)

    plt.tick_params(axis='both', which='major', labelsize=14)
    plt.tight_layout()

Device Failure Data

First, I loaded the data into a pandas dataframe to get some idea.

# readin the data into a dataframe
dateparser = lambda x: pd.datetime.strptime(x, "%Y-%m-%d")
df_raw = pd.read_csv("./device_failure.csv",
                     parse_dates = ["date"],
                     date_parser = dateparser,
                     encoding = "cp1252")

print("Shape: {}".format(df_raw.shape))
print("Prevalence = {:.3f}%".format(df_raw["failure"].sum()/df_raw.shape[0] * 100))

Shape: (124494, 12)
Prevalence = 0.085%

df_raw.head()

	date	device	attribute1	attribute2	attribute3	attribute4	attribute5	attribute6	attribute9
0	2015-01-01	S1F01085	215630672	56	0	52	6	407438	7
1	2015-01-01	S1F0166B	61370680	0	3	0	6	403174	0
2	2015-01-01	S1F01E6Y	173295968	0	0	0	12	237394	0
3	2015-01-01	S1F01JE0	79694024	0	0	0	6	410186	0
4	2015-01-01	S1F01R2B	135970480	0	0	0	15	313173	3

Preprocessing and builing X, Y training/testing sets.

target = "failure"
to_drop = ["date", "device", "attribute8", "failure"]
y = df_raw[target].values
X = df_raw.drop(to_drop, axis = 1)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, shuffle = True, random_state = 1367, stratify = y)
print(F"Train Size = {X_train.shape}")
print(F"Test Size = {X_test.shape}")

Train Size = (99595, 8)
Test Size = (24899, 8)

Printing the first 5 rows of the sclaed features.

X_train.head()

	attribute1	attribute3	attribute4	attribute5	attribute6	attribute9
7043	154658576	0	6	7	211825	1
115494	139749056	0	0	8	300480	0
42429	150809064	318	0	6	310486	18
35289	136377576	0	0	12	237584	0
57282	60144304	0	1	7	307632	0

Train a model

model = _clf_train(X_train, y_train, X_test, y_test)

[0]	validation_0-auc:0.594635
Will train until validation_0-auc hasn't improved in 20 rounds.
[1]	validation_0-auc:0.594635
[2]	validation_0-auc:0.618237
[3]	validation_0-auc:0.618237
[4]	validation_0-auc:0.618271
[5]	validation_0-auc:0.618271
[6]	validation_0-auc:0.618271
[7]	validation_0-auc:0.618271
[8]	validation_0-auc:0.617054
[9]	validation_0-auc:0.617054
[10]	validation_0-auc:0.662072
[11]	validation_0-auc:0.662072
[12]	validation_0-auc:0.662072
[13]	validation_0-auc:0.685412
[14]	validation_0-auc:0.685173
[15]	validation_0-auc:0.685164
[16]	validation_0-auc:0.685183
[17]	validation_0-auc:0.772991
[18]	validation_0-auc:0.773219
[19]	validation_0-auc:0.773221
[20]	validation_0-auc:0.773208
[21]	validation_0-auc:0.773261
[22]	validation_0-auc:0.773641
[23]	validation_0-auc:0.773637
[24]	validation_0-auc:0.773637
[25]	validation_0-auc:0.773635
[26]	validation_0-auc:0.773796
[27]	validation_0-auc:0.774048
[28]	validation_0-auc:0.773964
[29]	validation_0-auc:0.773948
[30]	validation_0-auc:0.773976
[31]	validation_0-auc:0.773968
[32]	validation_0-auc:0.773887
[33]	validation_0-auc:0.773855
[34]	validation_0-auc:0.773727
[35]	validation_0-auc:0.773725
[36]	validation_0-auc:0.773794
[37]	validation_0-auc:0.774106
[38]	validation_0-auc:0.774033
[39]	validation_0-auc:0.774095
[40]	validation_0-auc:0.77406
[41]	validation_0-auc:0.773846
[42]	validation_0-auc:0.773844
[43]	validation_0-auc:0.774055
[44]	validation_0-auc:0.773927
[45]	validation_0-auc:0.773927
[46]	validation_0-auc:0.773969
[47]	validation_0-auc:0.77399
[48]	validation_0-auc:0.774048
[49]	validation_0-auc:0.77426
[50]	validation_0-auc:0.814616
[51]	validation_0-auc:0.814617
[52]	validation_0-auc:0.814366
[53]	validation_0-auc:0.814277
[54]	validation_0-auc:0.814324
[55]	validation_0-auc:0.814311
[56]	validation_0-auc:0.814347
[57]	validation_0-auc:0.814238
[58]	validation_0-auc:0.814154
[59]	validation_0-auc:0.813977
[60]	validation_0-auc:0.813904
[61]	validation_0-auc:0.813735
[62]	validation_0-auc:0.811469
[63]	validation_0-auc:0.811915
[64]	validation_0-auc:0.811839
[65]	validation_0-auc:0.811803
[66]	validation_0-auc:0.811862
[67]	validation_0-auc:0.811875
[68]	validation_0-auc:0.811767
[69]	validation_0-auc:0.811832
[70]	validation_0-auc:0.81184
[71]	validation_0-auc:0.811859
Stopping. Best iteration:
[51]	validation_0-auc:0.814617

Visualization of Thresholds

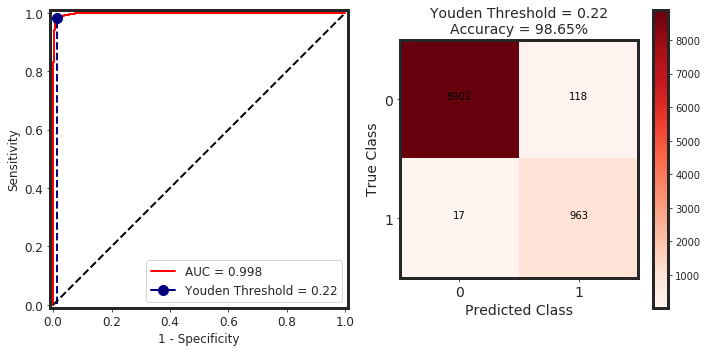
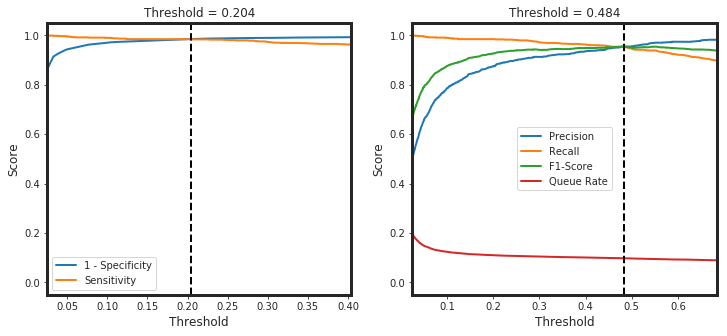
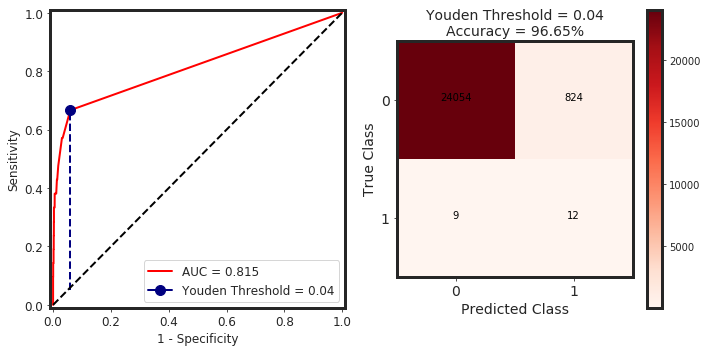
_threshold_finder(model = model, X = X_test, y_true = y_test)

png

MNIST DATA

from sklearn.datasets import fetch_openml
mnist = fetch_openml("mnist_784", version = 1)
mnist.keys()

dict_keys(['data', 'target', 'feature_names', 'DESCR', 'details', 'categories', 'url'])

X, y = mnist["data"], mnist["target"]
X.shape

(70000, 784)

plt.figure()
plt.imshow(X[1000].reshape(28, 28), cmap = "gray")
plt.show()

png

As you know, minist contains 10 classes. So, we need to turn this multi-class data to a binary class.

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]

y_train_0 = np.where(y_train == "0", 1, 0)
y_test_0 = np.where(y_test == "0", 1, 0)

model = _clf_train(X_train, y_train_0, X_test, y_test_0)

[0]	validation_0-auc:0.973597
Will train until validation_0-auc hasn't improved in 20 rounds.
[1]	validation_0-auc:0.97854
[2]	validation_0-auc:0.985121
[3]	validation_0-auc:0.984864
[4]	validation_0-auc:0.984705
[5]	validation_0-auc:0.986008
[6]	validation_0-auc:0.987206
[7]	validation_0-auc:0.988978
[8]	validation_0-auc:0.989422
[9]	validation_0-auc:0.989856
[10]	validation_0-auc:0.990381
[11]	validation_0-auc:0.990555
[12]	validation_0-auc:0.991208
[13]	validation_0-auc:0.991901
[14]	validation_0-auc:0.992248
[15]	validation_0-auc:0.993116
[16]	validation_0-auc:0.993295
[17]	validation_0-auc:0.99356
[18]	validation_0-auc:0.994208
[19]	validation_0-auc:0.994625
[20]	validation_0-auc:0.994797
[21]	validation_0-auc:0.994938
[22]	validation_0-auc:0.994881
[23]	validation_0-auc:0.995083
[24]	validation_0-auc:0.995208
[25]	validation_0-auc:0.995286
[26]	validation_0-auc:0.995402
[27]	validation_0-auc:0.995571
[28]	validation_0-auc:0.995561
[29]	validation_0-auc:0.995693
[30]	validation_0-auc:0.995979
[31]	validation_0-auc:0.996092
[32]	validation_0-auc:0.996214
[33]	validation_0-auc:0.996322
[34]	validation_0-auc:0.996352
[35]	validation_0-auc:0.99641
[36]	validation_0-auc:0.996402
[37]	validation_0-auc:0.996489
[38]	validation_0-auc:0.996557
[39]	validation_0-auc:0.996579
[40]	validation_0-auc:0.996637
[41]	validation_0-auc:0.996672
[42]	validation_0-auc:0.99685
[43]	validation_0-auc:0.996861
[44]	validation_0-auc:0.996935
[45]	validation_0-auc:0.996909
[46]	validation_0-auc:0.99693
[47]	validation_0-auc:0.996938
[48]	validation_0-auc:0.996977
[49]	validation_0-auc:0.997013
[50]	validation_0-auc:0.997113
[51]	validation_0-auc:0.99714
[52]	validation_0-auc:0.997175
[53]	validation_0-auc:0.997218
[54]	validation_0-auc:0.997237
[55]	validation_0-auc:0.997279
[56]	validation_0-auc:0.997314
[57]	validation_0-auc:0.997326
[58]	validation_0-auc:0.997386
[59]	validation_0-auc:0.997412
[60]	validation_0-auc:0.997424
[61]	validation_0-auc:0.997437
[62]	validation_0-auc:0.997439
[63]	validation_0-auc:0.997506
[64]	validation_0-auc:0.997521
[65]	validation_0-auc:0.997557
[66]	validation_0-auc:0.997573
[67]	validation_0-auc:0.997619
[68]	validation_0-auc:0.997634
[69]	validation_0-auc:0.997656
[70]	validation_0-auc:0.9977
[71]	validation_0-auc:0.997758
[72]	validation_0-auc:0.997782
[73]	validation_0-auc:0.997816
[74]	validation_0-auc:0.997846
[75]	validation_0-auc:0.997868
[76]	validation_0-auc:0.997896
[77]	validation_0-auc:0.997908
[78]	validation_0-auc:0.997916
[79]	validation_0-auc:0.997942
[80]	validation_0-auc:0.997937
[81]	validation_0-auc:0.997975
[82]	validation_0-auc:0.997996
[83]	validation_0-auc:0.998036
[84]	validation_0-auc:0.998106
[85]	validation_0-auc:0.998123
[86]	validation_0-auc:0.99815
[87]	validation_0-auc:0.998165
[88]	validation_0-auc:0.99818
[89]	validation_0-auc:0.998211
[90]	validation_0-auc:0.998225
[91]	validation_0-auc:0.998296
[92]	validation_0-auc:0.998316
[93]	validation_0-auc:0.998319
[94]	validation_0-auc:0.998359
[95]	validation_0-auc:0.998413
[96]	validation_0-auc:0.998415
[97]	validation_0-auc:0.998418
[98]	validation_0-auc:0.998432
[99]	validation_0-auc:0.99847

_threshold_finder(model = model, X = X_test, y_true = y_test_0)

png